Second example: Magnetostatic Interaction
This second example is a test if the demagnetising field is implemented correctly. To check this, we let 2 particles relax in the presence of an external field and check the output versus mumax. We also do the same simulation without calculating the demagnetising field to see if this problem is suited to check the implementation; i.e. to see that the demagnetising field makes a difference.
package main
import (
. "github.com/JLeliaert/vinamax"
)
func main() {
//Define the world at location 0,0,0 and with a side of 2e-6 m
World(0,0,0,2e-6)
//Adds two particles
Addsingleparticle(-64.48e-9,0,0)
Addsingleparticle(64.48e-9,0,0)
//the particles have radius 16 nm
Particle_radius(16e-9)
//external field along the x direction of 1mT
//B_ext can be an arbitrary function of time
B_ext = func(t float64) (float64, float64, float64) { return 0.001,0.,0.0}
//We calculate the demagnetizing field, but not with the FMM method
FMM=false
Demag=true
//set the saturation magnetisation of the particles
Msat (860e3)
//timestep : 1ps
Dt = 1e-12
//initialise time at zero
T = 0.
//temperature=0
Temp = 0.0
//Gilbert damping constant=0.1
Alpha = 0.1
//anisotropy constant=0
Ku1 = 0
//anisotropy axis along the z-direction
Anisotropy_axis(0, 0, 1)
//initialise the magnetisation along the y direction
M_uniform(0,1,0)
Tableadd("B_ext")
//write output every 1e-10s
Output(1e-10)
//Saves the geometry of the simulation
Save("geometry")
//run for 100 ns
Run(100.e-9)
}
The results of the simulation are visualised below and to validate the code, the comparison with Mumax3 of (@barnex) has been made. Also the solution to the same problem without including the demagnetising field is included to see that it makes a difference in this problem.
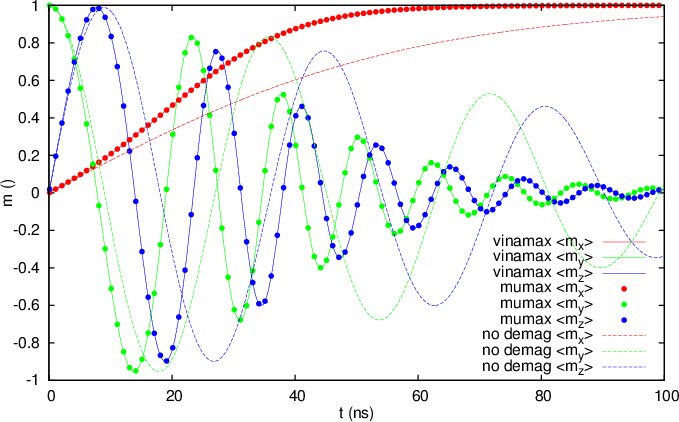
The output of the second example plotted with GNUPLOT