Third example: Fast Multipole Method
This example shows the agreement between the Fast Multipole Method implementation and the brute force implementation of the magnetostatic interaction. The same problem is also solved without taking this interaction into account so to show that it is of importance in this system.
package main
import (
. "github.com/JLeliaert/vinamax"
)
func main() {
//Defines the world at location 0,0,0 and with a side of 2e-6 m
World(0,0,0,2e-6)
//Adds a cube to the word with side 2e-6 m
test := Cube{S:2e-6}
//Adds 256 particles to the cube
test.Addparticles(256)
//the particle have radius 16 nm
Particle_radius(16e-9)
//external field along the x direction of 1mT
//B_ext can be an arbitrary function of time
B_ext = func(t float64) (float64, float64, float64) { return 0.001,0.,0.0}
//Calculate the demagnetizing field using the dipole approximation method
//the tresholdbeta= 0.4 is a good compromise between speed and accuracy
FMM=true
Thresholdbeta=0.4
Demag=true
//saturation magnetisation
Msat (860e3)
//timestep : 0.9ps
Dt = 5e-12
//initialise time at zero
T = 0.
//temperature=0
Temp = 0.00
//Gilbert damping constant=0.1
Alpha = 0.1
//anisotropy constant=0
Ku1 = 0
//anisotropy axis along the z-direction
Anisotropy_axis(0, 0, 1)
//initialise the magnetisation along the y direction
M_uniform(0,1,0)
//Adds the external field to the outputtable
Tableadd("B_ext")
//write output every 1.5e-10s
Output(1.5e-10)
//saves the geometry of the simulation
Save("geometry")
//calculates the tree for the dipole approximation
Maketree()
//run for 100 ns
Run(1.e-7)
//saves the magnetisation of the simulation
Save("m")
}
The results of the simulation are visualised below. The magnetisation calculated with and without the FMM method coincide, so both methods give the same result. Also, the result of the same system integrated without taking the demagnetising field into account results in a different magnetisation, so the demagnetising field is important in this system.
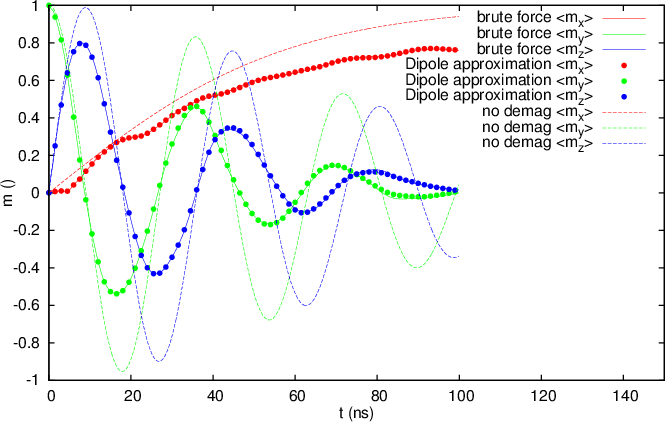
The output of the third example plotted with GNUPLOT