Sixth example: Relaxation
The diameter of the particles can be given a lognormal distribution. This example shows how an ensemble of 20000 particles which are initially magnetised in the z-direction relaxes towards a random (per particle) anisotropy direction.
package main
import (
. "github.com/JLeliaert/vinamax"
)
func main() {
//Defines the world at location 0,0,0 and with a side of 2e-5 m
World(0,0,0,2e-5)
//Adds a cube to the word with side 2e-5 m
test := Cube{S:2e-5}
//Adds 20000 particles to the cube
test.Addparticles(20000)
//the particles have a lognormal distribution of diameters
//with mean 20 nm and stdev 1 nm of the log of the diameters
Lognormal_diameter(20e-9, 1e-9)
//Don't calculate the demagnetsing field
Demag=false
//saturation magnetisation 860 000 A/m
Msat (860e3)
//timestep : 2ps
Dt = 2e-12
//initialise time at zero
T = 0.
//temperature=0
Temp = 0.0
//Gilbert damping constant=0.05
Alpha = 0.05
//anisotropy constant=10 000 J/m**3
Ku1 = 10000
//anisotropy axis is random for every particle
Anisotropy_random()
//initialise the magnetisation along the z direction
M_uniform(0,0,1)
//write output every 4e-12s
Output(4e-12)
//Save the magnetisation at the start of the simulation (to see the diameters)
Save("m")
//run for 20 ns
Run(20.e-9)
}
The results of the simulation are visualised below. The particles are initialised with their magnetisation parallel to the z-axis. They have a random anisotropy axis, so they relax towards this axis (above the horizontal plane) The average magnetisation thus relaxes towards 2/Pi. This value is the mean of cos(x) between O and pi.
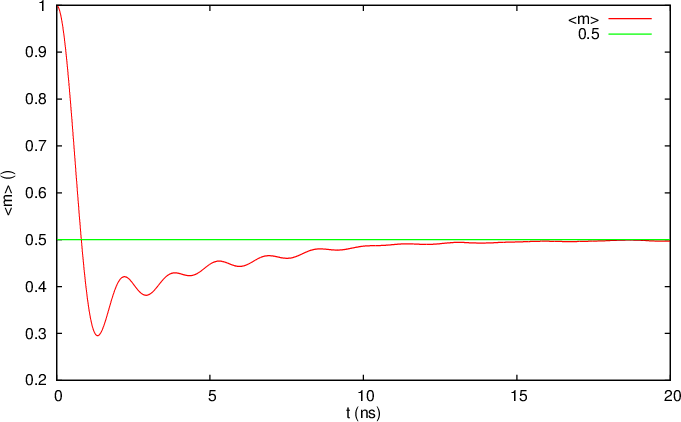
The output of the sixth example plotted with GNUPLOT
The diameters of the particles was taken from a lognormal distribution, to prove that this is implemented correctly, the distribution of the particles is shown, together with the theoretical curve they are supposed to follow.
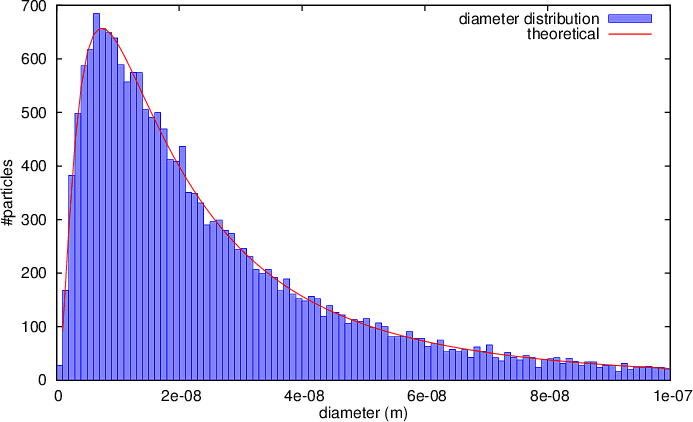
The distribution of the diameters of the particles in the sixth example plotted with GNUPLOT